
Back in 2009, the Race to the Top competitive grants incentivized Common Core curriculum. This new initiative would provide extra funding to the states adopting the Common Core standards and methodologies. While the changes to English are understandable, Common Core Math has boggled the minds of parents everywhere.
For many of us, math feels fairly straightforward. Unlike humanities, math problems have one right answer. Usually, there is no need for any justification for a correct answer. Moreover, there are methods to solving that generations of students have learned.
Why is Common Core replacing methods that are not broke? The answer lies in our current test scores. Unfortunately, American students are not performing well as compared to their counterparts in other countries. The difference is so stark that the Common Core standards became a necessary change towards bridging the gap.
To be more specific, however, Common Core is not actually replacing our tried-and-true methods. In fact, it is merely adding more methods that help illustrate the process behind many of our familiar methods.
But why are the Common Core Math problems so difficult to solve?
This is a fair question. A lot of the Common Core methods force a lot of seemingly extra or unnecessary effort in solving the problem. Why must students learn to do things the hard way—especially when the easier method works every time?
My ninth grade math teacher told my Algebra 2/Trig Honors class a secret. Mathematicians are lazy. It’s true; for every method we learn in math, there is usually a much simpler and straightforward way to solve the question. Usually, we learn this simpler way after we have mastered the harder way.
We can explain this logically. Without understanding the basics of the solutions, we cannot fully understand the mechanics of the simpler way of solving. For example, a tricycle or bicycle with training wheels is not a very useful mode of transportation. However, it is a necessary stepping stone to learn how to ride a bicycle properly.
This is exactly what Common Core Math is trying to do, albeit much earlier than usual in student’s math curriculum. To ensure that students have an explicit understanding of what addition, subtraction, multiplication, and division is, Common Core Math forces them to illustrate these operations. Since most students are visual learners, this is especially helpful.
Let’s take an example.
You have probably seen the following picture floating around on Facebook:

The “Frustrated Parent” above is using something we are all familiar with. It’s regular 3-digit number subtraction and it does not even require any borrowing. The method “Frustrated Parent” is using is called the standard algorithm.
Do not be alarmed! This standard algorithm is still being taught in Common Core Math curriculum. The point of learning (and teaching) this method is to ensure that the working and reasoning behind the standard algorithm is clear.
The Explanation:
The problem above wants the student to find the difference between 427 and 316 using a number line. This is the crux of the problem. The problem frames this question in the form of finding the mistake another student, “Jack’s”, solution as well as explaining to Jack how to get the right answer.
This combines two essential aspects of Common Core Math. Not only do the standards want the student to understand the mechanics behind math but they also want the student to be able to explain (in written words) the solution.
This is a result of Common Core standards wanting students to improve their technical writing skills as well as wanting to measure true progress in student performance. In fact, the Math section in the end-of-the-year online standardized tests in California often has essay questions that ask students to explain their answers.
Back to the question, here’s how you are supposed to solve it. First, we create a number line that starts from 316 and ends at 427.

Now, we will round up or down to more manageable numbers. Let’s round 316 up to 320 and round 427 down to 420. All the while, we will be recording the distances between these changes. This shows students that subtraction is nothing more than finding the distance between two numbers.

Finally, it is easy to see that the distance between 320 and 420 is 100. We can then add up the different distances we have to find the difference.
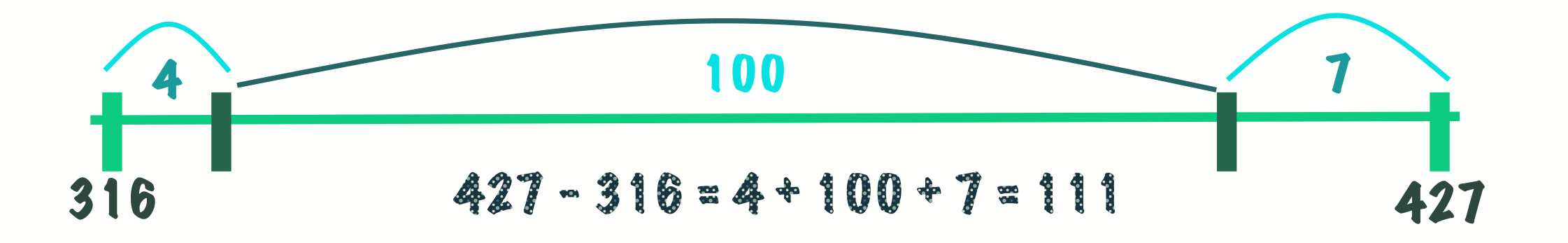
As we have solved above, the difference between 427 and 316 is the sum of the distances 4, 100, and 7 or 111. Disclaimer: The steps we chose above is only one combination of rounding. Students may choose other variations as they see fit.
How does Common Core affect higher levels of mathematics?
Now the problem explained above is fairly elementary math. To be frank, the methods only get more convoluted as the grade level increases. You can see the standards and method explanations for yourself here. After a certain point, if your student pursues any Advanced Placement mathematics or IB mathematics, the Common Core standards no longer apply.
However, if your child is still in elementary school, middle school, or in the early years of high school, these standards and methods still apply! Often, students will be lost and confused while navigating through these standards.
It is important for parents to equip themselves with the ability to help their child along the way. Unfortunately, few parents, although they are college-educated, have the time to develop this ability. Moreover, students who utilize methods unlike those taught in class are penalized on their tests.
We believe it is better to be safe than sorry. Hire a Common Core Math tutor who is an expert on all of these new methods. They will be able to ensure that the student does not struggle to understand some of these convoluted algorithms.
So, is Common Core Math good for students?
This is a mixed bag. On the one hand, Common Core Math implements methods to ensure that students have their basics mastered. On the other hand, it has not really shown the results that the government was expecting.
American students still fall behind in their test scores when it compared to their counterparts learning in other first-world countries and developing countries. Only time will tell whether this implementation will last long enough to see lasting impact on our students.